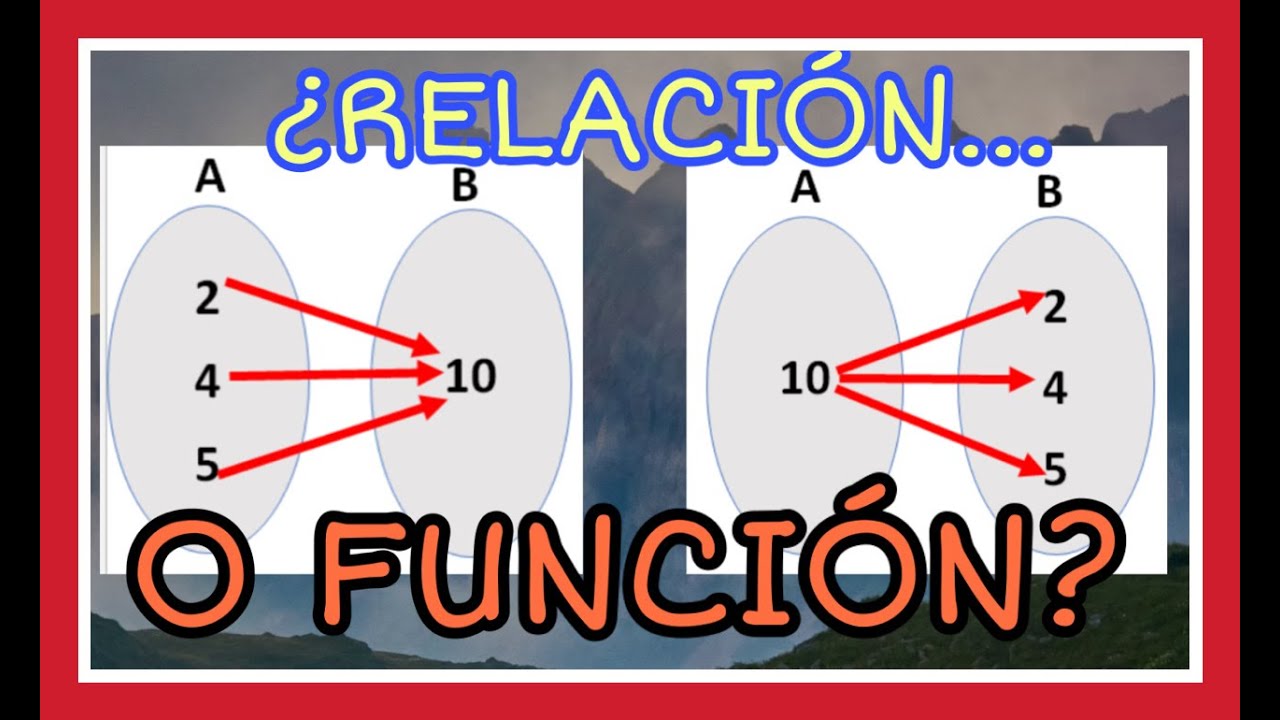
La diferencia entre función y relación es un concepto fundamental en diversas disciplinas, como la matemática, la física y la sociología. Aunque a primera vista pueden parecer similares, tienen características distintas que definen su naturaleza y aplicación.
¿Qué es una función?
En matemáticas, una función es una relación entre dos conjuntos, en la que a cada elemento del primer conjunto le corresponde un único elemento del segundo conjunto. Esta correspondencia se expresa mediante una regla que asigna a cada elemento de entrada (dominio) un valor de salida (codominio).
En otras palabras, una función establece una conexión precisa y determinada entre dos conjuntos, donde cada elemento de uno se relaciona exclusivamente con un elemento del otro. Esto implica que no puede haber duplicados en la correspondencia y que un mismo elemento de entrada siempre se asociará a un mismo elemento de salida.
Las funciones pueden representarse gráficamente en un plano cartesiano, donde el eje x representa el dominio y el eje y representa el codominio. Cada punto en el gráfico representa una pareja ordenada (x, y), donde x es el valor de entrada y y es el valor de salida.
En las ciencias exactas, las funciones son utilizadas para modelar fenómenos y resolver problemas. También son la base de otras ramas de las matemáticas, como el cálculo y el álgebra lineal.
¿Qué es una relación?
Por otro lado, una relación es una conexión entre dos o más elementos de conjuntos diferentes. A diferencia de las funciones, las relaciones pueden ser más generales y no están limitadas a una correspondencia uno a uno.
En las ciencias sociales y humanas, las relaciones son utilizadas para analizar la interacción entre individuos, grupos o instituciones. Por ejemplo, se pueden estudiar las relaciones familiares, las relaciones laborales o las relaciones diplomáticas entre países.
Una relación puede ser simétrica, asimétrica o reflexiva, dependiendo de la naturaleza de la conexión entre los elementos. Por ejemplo, en una relación de amistad, si una persona A es amiga de una persona B, la relación es simétrica si B también es amiga de A. Si la amistad es unilateral, la relación es asimétrica.
Las relaciones pueden ser representadas gráficamente mediante diagramas de Venn, que muestran la intersección entre los conjuntos y las conexiones entre sus elementos.
En resumen, una función es una relación uno a uno entre dos conjuntos, donde cada elemento de uno se relaciona con un único elemento del otro. Las funciones se utilizan en las ciencias exactas y se representan gráficamente en un plano cartesiano.
Por otro lado, una relación es una conexión entre elementos de conjuntos diferentes, que puede ser uno a uno o uno a muchos. Las relaciones se utilizan en las ciencias sociales y se representan mediante diagramas de Venn.
Es importante comprender la diferencia entre función y relación para aplicar correctamente estos conceptos en diversos campos y disciplinas.
1. ¿Puede una función ser una relación?
Sí, todas las funciones son relaciones, pero no todas las relaciones son funciones. Una función es una relación que cumple con la propiedad de correspondencia uno a uno.
2. ¿Puede una relación ser una función?
No necesariamente. Una relación puede ser una función si cumple con la propiedad de correspondencia uno a uno, pero también puede ser una relación uno a muchos o muchos a muchos.
3. ¿Para qué se utilizan las funciones en el campo de las ciencias exactas?
Las funciones son utilizadas para modelar fenómenos, resolver problemas y desarrollar otras ramas de las matemáticas, como el cálculo y el álgebra lineal.
4. ¿Cómo se representan gráficamente las relaciones?
Las relaciones pueden ser representadas mediante diagramas de Venn, que muestran la intersección entre los conjuntos y las conexiones entre sus elementos.